L’ultimo teorema di Fermat dimostrato su Libero?
Articolo di Luca Antonelli e Rosita Sormani
Su Libero del 9 maggio 2021 è comparso, in uno spazio a pagamento, un curioso pezzo che riporterebbe la dimostrazione matematica dell’ultimo teorema di Fermat. Si tratta di uno dei più noti teoremi matematici e la sua fama va ben oltre quella degli addetti ai lavori, anche grazie al suo enunciato semplice e facilmente comprensibile.
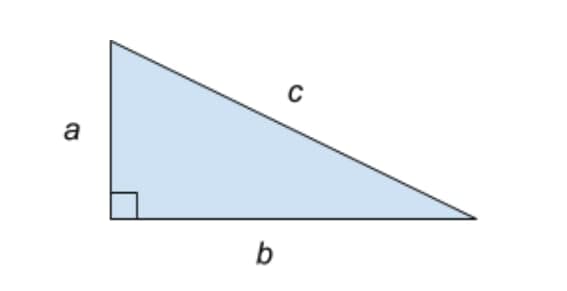
Fin dalla scuola primaria, tutti abbiamo imparato il teorema di Pitagora: in un triangolo rettangolo la somma dei quadrati dei due cateti (i due lati che formano l’angolo retto) è uguale al quadrato dell’ipotenusa (il lato più lungo, opposto all’angolo retto). Nel disegno sotto, a2+b2 = c2.
Le misure a, b e c dei tre lati possono valere qualunque numero positivo, ma è particolarmente interessante il caso in cui sono tutti numeri interi. Ad esempio, è possibile formare un triangolo rettangolo di lati 3, 4 e 5, e vale 32+42 = 52. Un altro esempio è il triangolo di lati 5, 12 e 13. Le terne di numeri interi di questo tipo, cioè che rispettano l’equazione a2+b2 = c2, sono dette terne pitagoriche e ne esistono infinite.
Ai matematici piace generalizzare le proprie affermazioni e molto presto si sono chiesti: che cosa succederebbe se invece del quadrato usassimo un’altra potenza intera? Ad esempio, esistono delle terne pitagoriche “cubiche” di numeri interi a, b, c, per cui a3+b3 = c3? Più in generale, esistono delle terne an+bn = cn per un qualunque numero intero n?
L’ultimo teorema di Fermat afferma che la risposta è no: se n è maggiore di 2 non esistono terne di numeri interi positivi che soddisfano l’equazione an+bn = cn, possiamo trovarle solo nel caso n=2.
Ma come si arriva a questo risultato? L’enunciato del teorema è molto semplice, ma la dimostrazione è stata una impresa di secoli, iniziata da Pierre de Fermat, il matematico francese che lo formulò all’incirca nel 1637. Fu il figlio di Fermat, dopo la sua morte, a ritrovare l’enunciato: nel margine di un libro, Fermat aveva scritto che
“è impossibile separare un cubo in due cubi, o una potenza quarta in due potenze quarte, o in generale, tutte le potenze maggiori di 2 come somma della stessa potenza. Dispongo di una meravigliosa dimostrazione di questo teorema, che non può essere contenuta nel margine troppo stretto della pagina”.
Il geniale ma disordinato Fermat non aveva trovato spazio a sufficienza per scrivere la dimostrazione!
Da allora molti tra i più grandi matematici della storia si sono cimentati nel tentativo di risolvere il problema, che per secoli portò il nome di “congettura di Fermat”, e negli anni sono riusciti a fornire la dimostrazione per alcuni casi particolari. Fermat stesso pubblicò successivamente una dimostrazione per il caso n=4, Eulero per n=3 e Adrien-Marie Legendre per n=5. Solo nel 1994 il britannico Andrew Wiles è riuscito a concludere una dimostrazione valida per qualsiasi n, che gli ha richiesto anni di lavoro, centinaia di pagine di formule e soprattutto la conoscenza di oggetti matematici molto avanzati, che all’epoca di Fermat non erano disponibili.
Qual era invece la dimostrazione elaborata da Fermat e mai ritrovata? Non potremo mai saperlo con certezza, ma è molto probabile che la sua dimostrazione fosse incompleta o errata. Ancora oggi però c’è chi si chiede se sia possibile trovare una dimostrazione “semplice”, alla portata delle conoscenze matematiche del XVII secolo.
Per il momento, queste speranze sono andate deluse, anche dalla dimostrazione pubblicata su Libero, che in parecchi passaggi non ha nemmeno l’apparenza di un ragionamento matematico rigoroso. Gran parte dell’articolo non prova nemmeno a dimostrare il teorema, ma si perde in affermazioni di vario genere, che nella migliore delle ipotesi sono corrette matematicamente ma non hanno alcuna attinenza con la dimostrazione e nella peggiore sono considerazioni personali e pseudo filosofiche sulla natura soggettiva o oggettiva dei numeri.
Proviamo comunque a seguire il ragionamento dell’autore. Vuole dimostrare che per n maggiore di 2 non esistono soluzioni intere positive all’equazione an+bn = cn e per farlo parte da un esempio. Applicando la formula (a+b)2 = a2+b2+2ab per calcolare il quadrato della somma di due numeri, che molti di noi ricorderanno dalle scuole medie o superiori, spiega che 62 = (4+2)2 = 42 +22+2·(4·2) = 36. Se rimuoviamo il doppio prodotto 2·(4·2), otteniamo ovviamente un numero più piccolo di 36: non possiamo scrivere 36 = 62 = (4+2)2 = 42 +22 = 16+4 = 20 perché il doppio prodotto 2·(4·2) ci rovina la festa. Quindi a2+b2 non sarà mai uguale ad (a+b)2, e se questo è vero per i quadrati a maggior ragione lo sarà per potenze più grandi, dunque il teorema di Fermat sarebbe dimostrato. Qui è dove iniziamo a non essere d’accordo: il ragionamento, seppure espresso in maniera confusa, sarebbe pressoché corretto se l’equazione contenuta nel teorema di Fermat fosse an+bn = (a+b)n, ma non è scritto da nessuna parte che c debba essere uguale ad a+b. Inoltre, l’autore stesso si contraddice poche righe dopo ammettendo l’esistenza di soluzioni a a2+b2 = c2.
Si propone allora di dimostrare che non ne esistono per potenze superiori a 2. Come mai riusciamo a costruirne per a2+b2 = c2? Grazie ad una curiosa caratteristica dei numeri dispari: ciascuno di essi si può scrivere come la differenza di due quadrati consecutivi. Ad esempio 3 = 22-12 = 4-1, oppure 5 = 32–22 = 9-4, e così via. Nella tabella raccogliamo alcuni esempi.
| 3 | 22-12 |
| 5 | 32–22 |
| 7 | 42–32 |
| 9 | 52-42 |
| 23 | 122–112 |
| 25 | 132-122 |
| 27 | 142-132 |
I numeri in grassetto sono due casi interessanti: 9 e 25, oltre ad essere dispari e quindi differenza di due quadrati, sono loro stessi dei quadrati. Ecco allora che abbiamo trovato due terne pitagoriche: da 9 = 32 = 52-42 si trova 32+42 = 52, cioè la già citata terna 3, 4, 5; allo stesso modo da 52 = 25 si trova la terna 5, 12, 13. Possiamo ripetere lo schema e ricavare una terna pitagorica per ogni numero dispari che sia anche un quadrato. Ce ne sono infiniti, e quindi abbiamo ottenuto un procedimento, o algoritmo, per generare quante terne pitagoriche vogliamo.
Questo procedimento fallisce con le potenze superiori a 2: ad esempio, non è in genere possibile scrivere qualunque numero dispari come differenza di due cubi consecutivi, dunque il nostro metodo si ferma qui. Per l’autore, questa è anche la fine della dimostrazione: non esistono terne con potenza 3 (o qualunque altra potenza) perché l’algoritmo che abbiamo usato per trovarle con le potenze di esponente 2 non è applicabile.
Possiamo accontentarci di questa affermazione? Certamente no! Potrebbe esistere un altro algoritmo in grado di estrarre le terne che cerchiamo, oppure le terne potrebbero esistere anche senza un algoritmo in grado di generarle: del resto, basterebbe trovarne anche solo una per invalidare il teorema. L’algoritmo descritto sopra non è in grado neppure di generare tutte le terne con potenza 2: ad esempio manca la terna 82+152 = 172 (esistono in effetti degli algoritmi in grado di generare qualunque terna pitagorica, ma non divaghiamo troppo). È un principio che i logici matematici conoscono molto bene: se da A segue B, in generale è scorretto dire che, in assenza di A, B non può esistere. L’assenza di A non ci permette di dedurre niente sullo stato di B, che potrebbe esistere o non esistere; o in altre parole se A è vero allora B è vero, ma se A è falso non possiamo dire nulla su B. Per esempio, se Luca è nato a Torino, allora è nato in Italia; ma se Luca non è nato a Torino, potrebbe essere nato in Italia oppure no.
Tornando alla dimostrazione, se conosciamo un metodo per generare delle soluzioni, allora ovviamente esistono; se invece non conosciamo un metodo le soluzioni potrebbero esistere oppure no, non possiamo saperlo solo sulla base di questa informazione. Andrew Wiles ha dimostrato che in effetti le terne con potenza maggiore di 2 non possono esistere, ma non lo ha fatto a partire dal nostro semplice algoritmo. Certo, potrebbe esistere una dimostrazione “semplice” dell’ultimo teorema di Fermat e un giorno qualche matematico potrebbe scoprirla, ma possiamo affermare con certezza che non potrà cavarsela con l’affermazione pubblicata a chiusura della pseudo dimostrazione pubblicata su Libero, dicendo che il ragionamento è “sufficiente alla bisogna, resta il dubbio di sapere se questa sia l’unica possibilità”, né sostenendo “di averlo fugato con alcune tabelle numeriche, che purtroppo qui non hanno spazio sufficiente”: la mancanza di spazio a disposizione non era una motivazione valida ai tempi di Fermat, non lo è diventata di certo ora.

Articolo ben scritto, con passaggi consequenziali ed esempi chiarificatori dei concetti espressi.
Da quanto riportato ho idea che l’autore ignoto (che è bene per lui e per gli altri che rimanga tale…) ritenga di far parte della categoria dei geni matematici misconosciuti dalla “scienza ufficiale”. Non altrimenti si spiega lo spreco di denaro nel far pubblicare a pagamento (!) la sua pretesa “dimostrazione” alla quale avrà probabilmente dedicato un tempo notevole per metterla a punto e corredarla di considerazioni “pseudo-filosofiche”.
Non so se il tempo impiegato da Antonelli e Sormani per illustrarla su Queryonline (e da me per commentare il loro articolo…) sia ben speso o sia anch’esso uno spreco di risorse. Sarà forse il primo caso se sarà servito, ma ne dubito, per dissuadere altri “geni incompresi” a fare mostra della propria incompetenza.
Con le sue elucubrazioni l’autore dimostra semplicemente di non avere chiara la differenza fra implicazione materiale e implicazione logica o, in altri termini, la differenza fra congettura e teorema.
Ho una dimostrazione semplice che si basa sulle proprietà delle sommatorie:
A^nC^n-B^n in quanto a partire da n=3 la derivata prima di Y=X^n è una curva.
Una profonda riflessione sulle proprietà delle potenze (e sulle parabole) e quindi sulle sommatorie mi ha permesso di creare la mia algebra a modulo complicato in cui il modulo è una funzione e non un numero. Grazie alla proprietà nota come somma telescopica esiste la possibilità di quadrare l’area sotto la derivata prima Y’=nX^{n-1} mediante rettangoli con base 1 ed altezza M_{n,X}= (X^n-(X-1)^n) (che chiameremo Gnomoni), quindi in generale A^n può essere scritta come:
A^n = \sum_{1}{A} M_{n,X} = \sum_{1}{A} (X^n-(X-1)^n)
e quindi l’Ultimo Teorema di Fermat come:
\sum_{1}{A} (X^n-(X-1)^n) = \sum_{1}{C} (X^n-(X-1)^n) – \sum_{1}{B} (X^n-(X-1)^n)
semplificando
\sum_{X=1}{A} (X^n-(X-1)^n) = \sum_{X=B+1}{C} (X^n-(X-1)^n)
shiftando:
\sum_{X=1}{A} (X^n-(X-1)^n) = \sum_{X=1}{C-B} ((X+B)^n-(X+B-1)^n)
La dismostrazione potrebbe finire quì: per chi sa leggere la matematica infatti appare subito chiaro che nelle condizioni imposte da Fermat: A >C-B e anche ((X+B)^n-(X+B-1)^n) > (X^n-(X-1)^n).
Per chi conosce le Sommatorie e le regole che le governano sa che il ridimensionamento del limite superiore cioè ingrassare (scalare) C-B fino a farlo diventare A (che equivale a moltiplicarlo per {A/(C-B)}, è possibile solamente modificando opportunamente TUTTI i termini della sommatoria, cioè dividendoli TUTTI per {A/(C-B)}.
Fermat invece ci chiede di modificare i SOLI termini dipendenti dall’indice X quindi:
Per il caso n=2 termine e limiti crescono/descrescono linearmente, quindi esiste la possibilità mediante un cambio di variabile di aggiustare limiti e termini per trovare infinite soluzioni.
Ma a partire da n=3 ingrassando di 1 (o 1/K) il limite superiore e dimagrendo i termini X dimendenti di 1, si ottiene un risultato DIVERSO per la sommatoria in quanto si modifica la pendenza delle curva. La somma a destra potrà essere pari a quella di sinistra solo nel caso banale di A=C, cioè nel caso in cui sia possibile aumentare i limite superiore di B e nel contempo dimagrire i termini di B (cioè barare al solitario):
\sum_{X=1}{A} 3X^2-3X+1 = ? \sum_{X=1}{C-B+1} 3(X+B-1)^2-3(X+B-1)+1
La dimostrazione passa per il cambio di variabile x=X/K e la comprensione di questa scrittura delle sommatorie che si trasformano in due integrali:
Lim_{K->infinito} \sum_{x=1/K}{A} 3x^2/K-3x/K^2+1/K^3 = Lim_{K->infinito} \sum_{x=1/K}{C-B+1/K} 3(x+B-1)^2/K-3(x+B-1)/K^2+1/K^3
In cui si vede che fino a quando 1/K non diventa un infinitesimo e quindi 1/K^2 e 1/K^3 spariscono in quanto infinitesimi di ordine superiore
Si avrà sempre che la curva di destra è troppo ripida rispetto a quella di sinistra
3x^2/K-3x/K^2+1/K^3 < 3(x+B-1)^2/K-3(x+B-1)/K^2+1/K^3
e quindi per quanto piccolo il passo 1/K approcciando il nuovo limite superiore (che si avvicina indefinitamente ad A senza raggiungerlo se non al limite) genera sempre un salto successivo troppo grande a quello necessario a raggiungerlo. Cioè B (se prendiamo A e C interi) è impacchettato fra due valori razionali che possono essere resi piccoli a piacere, cioè è un irrazionale. Maggiori dettagli quì:
https://www.researchgate.net/publication/364321320_The_FLT_Maruellous_proof_via_Inequality_CMA_and_Limits_Rev_13
io ho risolto varie equazioni di Fermat ritenute irrisolvibili.
Riguardo all’ultimo teorema di Fermat facendo riferimento alla definizione originaria di Fermat ho dimostrato facilmente che l’equazione ha soluzioni ad esempio per n intero uguale a 3.
La soluzione da me trovata e’ verosibilmente la stessa di Fermat mai trovata.
Il tutto e’ sul mio libro ebook kindle Amazon “NUMERI PRIMI e COMPLESSI nuove formule e teoremi” “Sviluppi del setaccio di Eratostene e dei teoremi di Fermat” pubblicato recentemente.
il segreto se cosi’ si vuol chiamare e’ l’enunciato originale di Fermat che pochi nella foga di dimostrarlo o trovare delle soluzioni per n≥ 3 analizzano con cura.
L’altro segreto (Gauss aveva mangiato la foglia) e’ che Fermat conoscesse i suoi polli per cui seguendo l’enunciato dimostro’ il teorema. Insomma lo scherzo del prete, tanta ilarita’ e presa in giro gioiosa per i post matematici.
Le soluzioni per n≥ 3 esistono e come e Fermat penso le avesse trovate.
Come le ho trovate io per l’ultimo teorema di Fermat ed altre equazioni di Fermat.
Tutti falliscono pensando che il teorema di Pitagora abbia soluzione solo per n= 2 e che applicando la sua formula per n > 3 non abbia soluzioni!
errato!
il teorema di Pitagora o meglio l’uguaglianza di i al quadrato con la somma di a al quadrato e b al quadrato vale anche per n>3.
esistono delle terne an+bn = cn per un qualunque numero intero n come esponente?
si esistono.
l’errore e’ che l’estensione a n uguale a 2 cioe’ un teorema di Pitagora non possa valere o essere applicato per n≥ 3.
io le soluzioni per n ≥3 le ho trovate
come ho trovato soluzioni ad altre equazioni di Fermat ritenute irrisolvibili.
penso che fermat lo sapesse ma pose il seguito ridendoci sopra sapendo che avrebbe fatto impazzire per secoli il matematico di turno!