La matematica dietro i nodi di cravatta
di Luca Antonelli
Quante persone si sono trovate in difficoltà al momento di annodare una cravatta? Molti di noi utilizzano questo accessorio solo saltuariamente e fanno fatica quando devono indossarne una. Un’alleata inaspettata giunge in nostro soccorso: la matematica. Può sembrare strano, nell’immaginario comune i matematici non sono persone molto affini alla moda, e ancor meno all’abbigliamento formale, ma è così.
Uno studio condotto Thomas Fink e Yong Mao, del gruppo di ricerca sulla teoria della materia condensata del Cavendish Laboratory di Cambridge, anni fa mostrò che i nodi di cravatta possono interessare diverse branche della matematica, dalla topologia al calcolo combinatorio alla teoria dei grafi. Nel 1999 un loro articolo sul tema apparve come scientific correspondence su Nature. [1]
Ma come si descrive matematicamente un nodo di cravatta? Se avete una cravatta a portata di mano, andatela a prendere, mettetevi davanti ad uno specchio, e analizzate i movimenti che fate per annodarla. Noterete che si possono dividere in tre tipologie fondamentali. La prima è il movimento in cui si porta l’estremità larga della cravatta verso sinistra; per semplicità abbreviamo questo movimento con S. La seconda è il movimento in cui si porta la stessa estremità verso destra, lo chiameremo D. Infine si può far passare l’estremità attraverso la zona centrale della cravatta, chiameremo questo movimento C. [2]
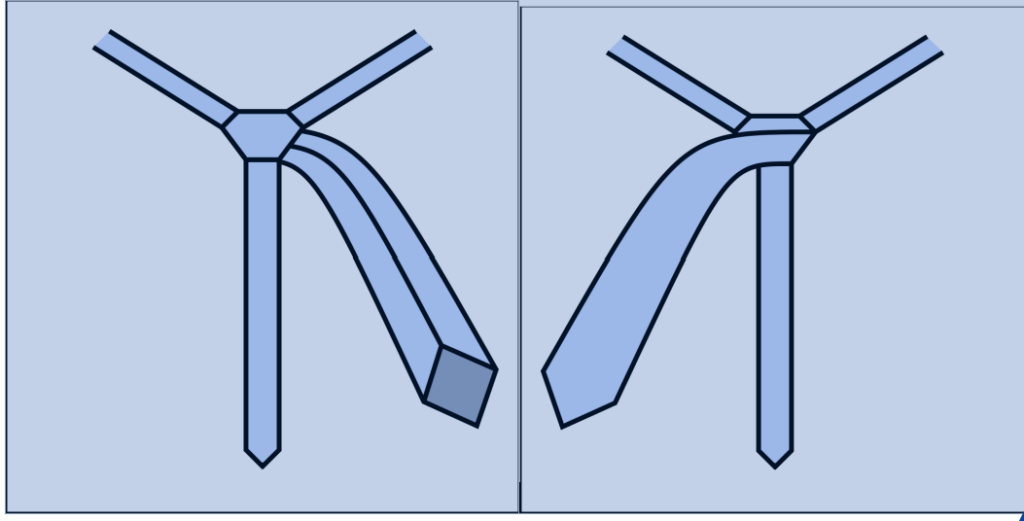
Ciascuno di questi movimenti si può fare in due direzioni. Ad esempio, nell’immagine a sinistra l’estremità della cravatta si trova sotto al nodo in costruzione, in direzione del vostro collo, e l’avvolgimento si ottiene facendola passare davanti al nodo stesso in direzione dello specchio. Al movimento successivo, nell’immagine a sinistra, qualunque movimento scegliate tra S, D e C, l’estremità sarà davanti al nodo, e dovrà necessariamente passare dietro, e così via, in un’alternanza di avvolgimenti davanti e dietro al nodo.
Al termine del processo, bisogna eseguire l’annodatura facendo passare la cravatta attraverso il nodo centrale. L’annodatura è un movimento separato, sempre uguale per tutti i nodi, che possiamo abbreviare con la lettera A.
Ora abbiamo un modo rapido per ricordare ogni nodo. Ad esempio, per realizzare il nodo Windsor basta eseguire la sequenza:
SCDSCDSCA
Il Windsor, noto in Italia anche come Scappino dal nome dell’omonima casa di moda, è considerato un nodo impegnativo, adatto a occasioni formali. Se desiderate un nodo meno voluminoso, ecco la ricetta per il “mezzo Windsor”:
SDCSDCA
Scrivere i movimenti come lettere non è soltanto un artificio mnemonico. Esprimere in maniera simbolica la realtà ci permette di astrarre il problema iniziale, studiarlo con gli strumenti della matematica e ricondurlo ad altri problemi noti.
Ad esempio, possiamo chiederci: quanti nodi di cravatta è possibile creare? Se pensassimo a questo problema in termini concreti, utilizzando delle vere cravatte, difficilmente arriveremmo alla soluzione: dovremmo provare tutti i possibili annodamenti e tenerne traccia, annotandoli o meglio ancora disegnandoli su un foglio, e ogni volta confrontare il nodo che stiamo provando per verificare di non averlo già prodotto.
Se invece rappresentiamo i nodi come sequenze di lettere, la nostra domanda diventa equivalente a “quante sequenze posso creare combinando le tre lettere S, D e C?” (l’annodamento finale A è lo stesso per tutti i nodi, e non influisce sul numero di sequenze, pertanto possiamo ignorarlo). Questo tipo di problemi si possono risolvere abbastanza facilmente grazie al calcolo combinatorio.
Fink e Mao diedero la risposta nell’articolo pubblicato su Nature nel 1999, tenendo conto di alcuni vincoli fisici nell’annodamento:
- il primo movimento non può essere del tipo C, dato che non c’è ancora l’anello centrale in cui far passare l’estremità della cravatta;
- si può stabilire che per convenzione il primo movimento è sempre S, verso sinistra; infatti, nella sequenza basta invertire D ed S e si ottiene lo stesso nodo “allo specchio”;
- non si possono mai fare consecutivamente due movimenti dello stesso tipo; ad esempio, se l’ultimo movimento è stato del tipo S, l’estremità della cravatta si trova già a sinistra e non posso ripetere il movimento;
- i movimenti finali prima dell’annodamento devono essere SDC o DSC, altrimenti non si creano le condizioni necessarie per l’annodatura di chiusura.
Inoltre, Fink e Mao hanno preso in considerazione solo nodi con un numero di movimenti compreso tra 3 e 9, escluso l’annodatura finale. Questo è un limite arbitrario e non dettato da limiti fisici, ma ragionevole: con meno di 3 movimenti non si annoda niente, mentre un nodo con più di 9 movimenti richiederebbe una cravatta lunghissima, oltre ad essere sproporzionato e scomodo da indossare.
Per chi è a proprio agio con le formule, riportiamo come calcolare esattamente il numero di possibili nodi facendo n movimenti:
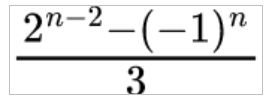
Facendo i calcoli, questi sono i risultati:
| Numero di movimenti | Nodi di cravatta possibili |
| 3 | 1 |
| 4 | 1 |
| 5 | 3 |
| 6 | 5 |
| 7 | 11 |
| 8 | 21 |
| 9 | 43 |
Abbiamo la risposta: il calcolo combinatorio ci dice che i nodi a nostra disposizione sono 1 + 1 + 3 + 5 + 11 + 21 + 43 = 85. I nodi di cravatta che si utilizzano abitualmente sono però molti di meno. Perché la moda, che in genere accoglie volentieri le novità, non ha mai considerato gli altri nodi? Secondo Fink e Mao, nella scelta dei nodi occorre tenere conto di alcune considerazioni estetiche, che si possono riassumere in due parole: simmetria ed equilibrio.
Ad esempio, la quantità di movimenti a destra e sinistra non può differire troppo, altrimenti il nodo risulterà storto. Allo stesso modo, la quantità di avvolgimenti orari e antiorari deve essere equilibrata, o il nodo finale non sarà abbastanza compatto. Applicando queste restrizioni, il numero di nodi “esteticamente corretti” si riduce a 13. I nodi di cravatta utilizzati diffusamente sono ancora meno, gli autori ne contano 4 o 5 al massimo, e propongono i restanti 9 per gli amanti della moda. Li riportiamo qui per i più curiosi che si volessero cimentare. [3] Molte altre informazioni e i restanti 72 nodi si possono trovare nel libro di Fink e Mao “85 modi di annodare la cravatta”. [4]
| Nodo | Movimenti |
| Small knot | SDCA |
| Four-in-hand | SDSCA |
| Kelvin | SDSDCA |
| Nicky | SCDSCA |
| Victoria | SDSDSCA |
| Half-Windsor | SDCSDCA |
| St Andrew | SDSCDSCA |
| Plattsburgh | SCDCSDCA |
| Cavendish | SDSCDSDCA |
| Windsor | SCDSCDSCA |
| Grantchester | SDSDCSDSCA |
| Hanover | SDCSDCSDCA |
| Balthus | SCDCSCDSCA |
Note
- [1] T. Fink, Y. Mao, Designing tie knots by random walks, Nature 398, 1999.
- [2] Utilizziamo qui la notazione semplificata riportata da Andrea Centomo e Giovanni Paolini (https://www.giovannipaolini.org/static/files/cravatte.pdf)
- [3] https://en.wikipedia.org/wiki/The_85_Ways_to_Tie_a_Tie
- [4] Il libro non è ristampato da tempo, è ancora reperibile, ma solamente di seconda mano; un po’ più semplice ed economico è recuperare la versione originale in inglese The 85 Ways to Tie a Tie.
Immagine di apertura: Foto di Tima Miroshnichenko da Pexels

